Tout d’abord, il est important de se souvenir de certains aspects fondamentaux lors de la résolution de ce type de problème.

+ multiplié/divisé par + donne +

La règle des signes

+ multiplié/divisé par – donne –

– multiplié/divisé par – donne +

Par exemple, si nous rencontrons un problème comme celui-ci :

-(+4) + (+6) – (-2) = x

Le résultat est -4 +6 +2 = 4

(-2)² + (-3)³ – (2)³ = x

(-2) x (-2) + (-3) x (-3) x (-3) – (2) x (2) x (2) = x

4 -27 -8= – 31

N’oubliez pas qu’un facteur négatif entre parenthèses changera tous les facteurs.

Fractions

Comme vous le savez, les fractions peuvent être additionnées, soustraites, multipliées ou divisées, chaque opération est effectuée de manière différente.

Multiplication des fractions : dans ce cas, nous multiplierons les numérateurs avec les numérateurs et les dénominateurs avec les dénominateurs.

Exemple : 5/7 x 3/6 = 15/42

Division des fractions : dans ce cas nous multiplierons le numérateur de la première fraction par le dénominateur de la deuxième fraction et placer le résultat dans le numérateur de la fraction résultante.

Ensuite, nous multiplierons le dénominateur de la première fraction par le numérateur de la deuxième fraction et placerons le résultat dans le dénominateur de la fraction résultante.

Exemple : 5/7 : 3/6 = 30/21

Addition et soustraction de fractions : nous devons trouver le plus petit dénominateur commun (PPDC) dans les deux fractions (le dénominateur commun sera le plus petit multiple des deux dénominateurs donnés).

2/5 + 4/3=

Dans ce problème, le PPDC est 15, nous devrons donc ajouter les deux fractions avec un dénominateur commun, dans ce cas 15.

Pour placer le numérateur, nous devons diviser le dénominateur précédent par le PPDC (15/5=3) et le résultat sera multiplié par le dénominateur (3×2=6), alors le résultat de la première fraction est 6/15.

Pour la deuxième fraction, la même procédure doit être effectuée, laissant :
6/15 + 20/15 = 26/15

Dans le cas de soustractions, la procédure à suivre serait la même.
5/2 – 5/6 = 15/6 – 5/6 = 10/6

Puissance d’un nombre

Une puissance dont l’exposant est « 0 »
son résultat sera toujours « 1 ».
Ex : 6⁰ = 1

Une puissance dont la base est « 1 » son résultat sera toujours « 1 ». Ex : 1⁵ = 1

Une puissance dont l’exposant est « 1 » son résultat sera toujours égal à la base. Ex : 8¹ =8

Une puissance dont la base est « 0 » son résultat sera toujours « 0 ». Ex : 0⁴ =0

Calcul mathématique par approximation

Au moment d’effectuer des exercices d’opérations mathématiques, nous pouvons trouver des opérations qui peuvent nous prendre un certain temps à effectuer, il est recommandé de revoir d’abord les options de réponse.

Par exemple :
862 x 376 = ?

a) 12017
b) 324112
c) 54231
d) 93421

Dans ce cas, nous voyons comment la seule option possible serait b, car pour les autres il est impossible que le résultat de cette opération soit à 5 chiffres. Pour le voir plus facilement, vous pouvez utiliser un calcul d’approximation, par exemple 800 x 400 = 320000

Une autre façon de résoudre rapidement des exercices mathématiques est de savoir par quel nombre cette opération se termine, ce qui permet souvent d’éliminer des réponses. Dans l’exemple précédent, nous voyons que l’opération doit se terminer par le nombre 2, puisque 2 x 6 = 12.

Si vous ne savez pas comment trouver la solution, recherchez parmi les réponses.

Par exemple :
la somme de deux nombres est 44 et leur différence est 10. De quel nombre s’agit-il :

a) 15-26
b) 9-36
c) 23-21
d) 27-17

Ici, au lieu de poser une équation, il est préférable de vérifier les réponses et, ainsi, nous voyons que a) et b) ne sont pas valides car les nombres des deux réponses ne donnent pas 44 comme indiqué par le problème. Le c) n’est pas non plus valable car bien qu’ils ajoutent 44 la différence n’est pas 10.

La priorité des opérations

1. D’abord, nous devons résoudre les opérations qui se trouvent entre crochets ou entre parenthèses.

2. Nous résolvons les racines et les puissances.

3. Ensuite, nous résolvons les divisions et les multiplications

4. Enfin, les additions et les soustractions.

(2-4×2)² + (8-2) – (3+3×3-1) = ?
-> (2 – 8)² + 6 – (3 + 9 – 1) = 36 + 6 – 11 = 31

Si nous avons plusieurs opérations suivies de la même priorité, nous les ferons toutes de gauche à droite.

Exemple : 4×4/2×3 = 16/2×3 = 8×3 =24

Vous devez essayer de faire des comptes mentaux rapidement et efficacement. Et ne prenez le stylo que lorsqu’il est indispensable car cela vous permettra d’avancer plus vite.

Astuces mathématiques

1. Calculer 50% revient à diviser par 2
50% de 230 = 115

2. Calculer 25% revient à diviser par 4
25% de 230 = 57.5

3. La multiplication par 0.5 à diviser ce nombre par 2
230 x 0.5 = 230 : 2 = 115

4. La multiplication par 0.25 à diviser ce nombre par 4
230 x 0.25 = 230 : 4 = 57.5

5. La division par 0.5 revient à multiplier ce nombre par 2
230 : 0.5 = 230 x 2 = 460

6. La division par 0.25 revient à multiplier ce nombre par 4
230 / 0.25 = 230 x 4 = 920

7. Pour multiplier par 5, nous ajoutons un zéro à la quantité, puis nous la divisons par deux
230 x 5 = 2300 : 2 = 1150

8. Pour diviser par 5, nous divisons la quantité par 10, puis multiplions par deux
230 : 5 = 23 x 2 = 46

9. Multiplication par onze
Une façon de multiplier par 11, c’est d’abord de le faire par 10, puis de l’additionner avec le nombre à multiplier :

5436 x 11 = 5436 x 10 + 5436 = 54360 + 5436 = 59796

10. Multiplication par quinze

1. On divise par 2 le nombre à multiplier
2. On additionne le nombre à multiplier au résultat de l’opération précédente
3. On multiplie par 10

28 x 15 = ?
-> 28 : 2 = 14
-> 14 + 28 = 42
-> 42 x 10 = 420

11. Division par quinze

1. On divise le nombre par 10
2. Puis on divise le résultat par 3
3. Enfin on le multiplie par deux

1890 : 10 = 189 : 3 = 63 x 2 = 126

12. Multiplication par vingt-cinq

1. On divise le nombre par 4
2. Le résultat est multiplié par 100

16 x 25 = 16 : 4 = 4 x 100 = 400

13. Division par 25

1. On divise le nombre par 100
2. On multiplie le résultat par 4

650 : 100 = 6.5 x 4 = 26

14. Division par 2
Les nombres pairs sont toujours divisibles par 2.

15. Division par 3
Un nombre est divisible par trois si la somme de ses nombres est divisible par trois.

Exemple : 42111 : 3
-> 4 + 2 + 1 + 1 + 1 = 9 est divisible.

16. Division par 4

Un nombre est divisible par 4 si la somme des deux derniers chiffres est divisible par 4, ou se termine par 2 zéros ou plus.

Exemple : 5322 est divisible par 4 car 2 + 2 = 4.

17. Division par 5

Un nombre est divisible par 5 s’il se termine par 0 ou 5

18. Division par 6

Un nombre sera divisible par 6 s’il maintient à la fois des conditions de division par 3 et de division par 2.

19 Division par 8

Un nombre est divisible par 8 si la somme des trois derniers chiffres est divisible par 8 ou se termine par 3 zéros.

20. Division par 10

Un nombre se terminant par 0 est toujours divisible par 10.

21. Division par 11

Un nombre est divisible par 11 lorsqu’il la somme des nombres en position impaire et la somme des nombres en position paire sont égales.

Exemple :
Est-ce que 25795 est divisible par 11 ?
Nombres en position paire = 5 et 9
nombres en position impaire = 2, 7 et 5
-> 5 + 9 = 2 + 7 + 5 donc 25795 est divisible par 11.

22. Division par 12
Un nombre sera divisible par 12 s’il remplit à la fois les conditions de division par 4 et de division par 3.

23. Division par 15
Un nombre sera divisible par 15 s’il remplit à la fois les conditions de division par 5 et de division par 3.

Calculs avec les pourcentages

Pour calculer le pourcentage d’une quantité, le pourcentage est divisé par 100 et le résultat est multiplié par la quantité.

15% de 2400 = ?
-> 15 : 100 = 0,15 x 2400 = 360

Si le pourcentage entre 2 quantités doit être trouvé. Le moyen le plus rapide consiste à soustraire les deux quantités et une simple “règle de trois” est établie avec la quantité résultante et la plus grande des deux quantités initiales, le résultat est le pourcentage qui les sépare.

Si quelque chose coûte 20 000 € et coûte maintenant 16 000 €, quel est le pourcentage de remise ?

20000 – 16000 = 4000
20000 -> 100 %
4000   -> X %

X= (4000 x 100) / 20000 = 20 %

Nous devons calculer combien un autre prix devient, si un pourcentage augmente ou diminue, il y a deux façons :

Si à 133 € on l’augmente de 26%, quel serait le nouveau prix de X ?

X = 133 + 26% x 133

• X = 34,58 + 133 + = 167,58

Deuxième option (plus rapide)

133 -> 100%
X     -> 126%

• X = 133 x 126 / 100 = 167,58

Calculer une quantité X sachant que 41% X = 214

41%   -> 214
100% -> X

• X = (214 x 100) / 41= 521,95

Exercices de distribution proportionnelle

Distribuer en parties directement proportionnelles 1260 € à 3, 5 et 2

3X + 5X + 2X = 1.260

10X = 1.260

X = 1.260/10 = 126

3X = 3 x 126 = 378

5X = 5 x 126 = 630

2X = 2 x 126 = 252

Exercices de distribution inversement proportionnelle

Il est important de diviser en parties inversement proportionnelles 3, 4 et 2.

Elle se fait de la même manière que la précédente mais avec les inverses.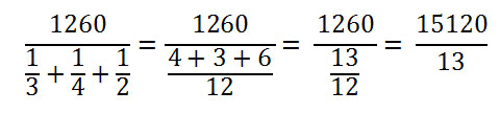

Ensuite, nous multiplions cette quantité par l’inverse qui correspond à chacun.

15120/13 x 1/3 = 387,69

15120/13 x 1/4 = 290,77

15120/13 x 1/2 = 581,53

Exercices sur la règle de trois

Ces exercices peuvent être à la fois sur la règle de trois inverse et directe. La règle directe, se réfère à la règle de 3 qui en augmentant l’un, augmente l’autre. L’inverse, à mesure que l’un augmente, l’autre diminue.
Voyons cela avec des exemples :

Si nous savons que 6 livres valent 14 €, combien d’euros valent 10 livres ?

Dans ce cas, ce serait une règle de trois directe et il serait multiplié transversalement et divisé par l’autre nombre. Le problème se pose alors comme suit :

6 livres   —– 14 €
10 livres —— x

10 x 14 / 6 = 23, 33€

Si 3 ouvriers construisent une maison en 40 jours. En combien de jours 10 ouvriers construiraient-ils la même maison ?

Dans ce cas, ce serait une règle de trois inverses et il faudrait multiplier dans une rangée et diviser par l’autre nombre. Le problème se pose comme suit :

3 ouvriers ——- 40 jours

10 ouvriers ——- x jours

3 x 40/10 = 12 jours

Réglé de trois avec 3 variables

La formule pour ce type de problème serait :

Il est utilisé dans des problèmes tels que : si un groupe de 10 travailleurs coupe 8 arbres en 16 jours, combien de jours 6 travailleurs pourront-ils couper 10 arbres ?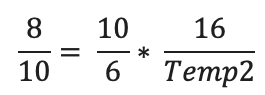

Temps2 = 33,3 jours

Exercices sur intervalles numérique

Ces exercices demandent combien de nombres se trouvent entre deux nombres. Bien qu’au début ils peuvent sembler très faciles, ils peuvent s’avérer être assez difficiles. Voyons les astuces qui peuvent être utilisées pour résoudre ces exercices beaucoup plus rapidement.

Tout d’abord, nous devons savoir que ces exercices peuvent être proposés de plusieurs manières. Cela comprend :

1. Combien de nombres y a-t-il entre deux numéros ouverts.
       (n1 – n2) + 1 = R

       Combien de nombres y a-t-il entre 32 et 121 ouverts ?  

       (121 – 32) + 1 = 89 +1 = 90

2. Combien de nombres se trouvent entre deux nombres fermés.
       (n1 – n2) – 1 = R

Combien de nombres y a-t-il entre 32 et 121 fermés ?
(121 – 32) – 1 = 89 -1 = 88

3. Combien de nombres y a-t-il entre deux numéros ouverts, sans compter les nombres pairs

• On fait d’abord la soustraction normale avec cette formule
  (n1 – n2) + 1 = R
  
  
• Il faudrait alors prendre en compte plusieurs variables

a. n1, n2 pairs :  R – 1

b. n1, n2 impairs : R + 1

c. n1, n2 pairs et impairs, nous ne devons rien additionné à R.

d. Finalement, le résultat = R / 2

           Exemple :

  Combien de nombres y a-t-il entre 32 et 121 ouverts, sans
  compter les nombres pairs ?
  (121 – 32) + 1 = 89 +1 = 90

           Puisque les nombres sont un pair (32) et un impair (121), nous

           ne devons rien additionner et nous divisons soit 90/2 = 45

4. Combien de nombres y a-t-il entre deux numéros ouverts, sans compter les nombres impairs.

• On fait d’abord la soustraction normale avec cette formule
           (n1 – n2) + 1 = R
  
  
• Il faudrait alors prendre en compte plusieurs variables

       a. n1, n2 pairs :  R + 1

       b. n1, n2 impairs : R – 1

       c. n1, n2 pairs et impairs, nous ne devons rien additionné à R.

       d. Finalement, le résultat = R / 2

5. Combien de nombres se trouvent entre deux nombres fermés, sans compter les nombres pairs.

• On fait d’abord la soustraction normale avec cette formule
           (n1 – n2) – 1 = R
  
  
• Il faudrait alors prendre en compte plusieurs variables

       a. n1, n2 pairs :  R – 1

       b. n1, n2 impairs : R + 1

       c. n1, n2 pairs et impairs, nous ne devons rien additionné à R.

       d. Finalement, le résultat = R / 2

       Exemple :

       Combien de nombres y a-t-il entre 32 et 121 fermés, sans

       compter les nombres pairs ?

       (121 – 32) – 1 = 89 -1 = 88.

       Puisque les nombres sont un pair (32) et un impair (121), nous ne

       devons rien additionner et nous divisons soit 88/2 = 44.

6. Combien de nombres se trouvent entre deux nombres fermés, sans

    compter les nombres impairs.

• On fait d’abord la soustraction normale avec cette formule
           (n1 – n2) – 1 = R
  
  
• Il faudrait alors prendre en compte plusieurs variables

       a. n1, n2 pairs :  R + 1

       b. n1, n2 impairs : R – 1

       c. n1, n2 pairs et impairs, nous ne devons rien additionné à R.

       d. Finalement, le résultat = R / 2

       Combien de nombres y a-t-il entre 32 et 121 fermés, sans

       compter les nombres impairs ?

        (121 – 32) – 1= 89 -1 = 88

       Puisqu’un nombre pair (32) et un nombre impair (121)

       n’additionnez rien, et nous divisons soit 88/2 = 44

       Comme vous pouvez le voir, ces types d’exercices peuvent

       sembler un peu désordonnés au début, mais avec de la pratique,

       ils sont résolus très rapidement.

Géométrie

Nous pouvons également trouver des exercices liés à la géométrie, en particulier il est extrêmement important de savoir comment trouver l’aire et le périmètre des éléments géométriques les plus importants.

Carré
Périmètre = côté x 4
Aire = côté du carré x côté du carré

Rectangle
Périmètre = 2 x (largeur + hauteur)
Aire = largeur x hauteur

Triangle
Périmètre = somme des 3 côtés
Aire = (base x hauteur) / 2

Cercle
Périmètre = 2 x π x r, où r est le rayon
Aire = π x r2

Exercices sur l’âge et les portions

Dans ce type d’exercice il faut proposer un système d’équations et donc prendre les données qui nous sont demandées.

Exemple :

Juan, Sara et Virginia ont respectivement 4, 6 et 11 ans et leur père a 35 ans. Combien d’années faut-il pour que la somme des âges des enfants soit égale à celle du père ?

Dans ce type d’exercice, une équation doit être formulée comme suit :

(4 + x) +(6 + x) +(11 + x) = 35 + x
-> 21 + 3x = 35 + x
-> 3x – x = 35 – 21
-> x = 14/2 = 7

Système métrique

Unités de longueur

Myriamètre (mam) –> 10 000 mètres

Le kilomètre (km) –> 1 000 mètres.

L’hectomètre (hm) –> 100 mètres.

Le décamètre (dam) –> 10 mètres.

Le décimètre (dm) –> 0,1 mètre.

Le centimètre (cm) –> 0,01 mètre.

Le millimètre (mm) –> 0,001 mètre.

Unités d’aire

Myriamètre carré (Mm2) -> 100 000 000 m2

Kilomètre carré (km2) -> 1 000 000 m2

Hectomètre carré (Hm2) ou Hectare (HA) -> 10 000 m2

Décamètre carré (Dm2) ou Surface (A) -> 100 m2

Mètre carré (m2) -> 1 m2

Décimètre carré (dm2) -> 0,01 m2

Centimètre carré (cm2) -> 0,00001 m2

Millimètre carré (mm2) -> 0,000001 m2

Unité de mesure de capacité

Kilolitre (Kl) -> 1000 l

Hectolitre (Hl) -> 100 l

Décalitre (Dl) -> 10 l

Litre (l) -> 1 l

Décilitre (dl) -> 0,1 l

Centilitre (cl) -> 0,01 l

Millilitre (ml) -> 0,001 l

Unité de masse

Ton (Tm) -> 1,000,000 gr

Quintal (q) -> 100.000 gr

Kilogramme (Kg) -> 1000 gr

Hectogramme (Hg) -> 100 gr

Décagramme (Dg) -> 10 gr

Gramme (gr) -> 1 gr

Décigramme (Dg) -> 0,1 gr

Centigramme (cg) -> 0,01 gr

Milligramme (mg) -> 0,001 gr

Unités de mesure anglo-saxonnes

1 mil = 25,4 µm (micromètres)

1 pouce (inch) = 2,54 cm

1 pied (foot) = 12 pouces = 30,48 cm

1 verge (yard) = 3 pieds = 91,44 cm

1 once (oz) = 16 drachmes = 28,34952312495957 g

1 livre (lb) = 16 oz = 453 5923699993531 g

Pinte (pt) = 550,610471358 cm³ (ml)

1 pouce carré (sq in ou in²) = 6,4516 cm²

1 pied carré (pi ou pi²) = 144 pi² = 929.0304 cm²

Concepts statistiques importants

Moyenne : Elle est utilisée pour obtenir la moyenne de différentes grandeurs. Elle est calculée en additionnant toutes les grandeurs et en le divisant par le nombre de toutes.

Médiane : Il s’agit de la valeur centrale d’une série de données ordonnée par sa valeur. Si le nombre était pair, il faudrait obtenir la moyenne arithmétique des deux valeurs centrales.

Mode : C’est le nombre qui apparaît le plus de fois dans une série de valeurs.